第二部分:深入下潜ARIMA
继续时间序列分析深入跳入时间序列模型ARIMA,这是数据科学领域常用的重要平滑技术
万一你读不读第一部分数列时序概论自便
七.ARIMA自回归集成平均移动
ARIMA表示自动递归综合移动平均值模型旨在描述数据相互关系可使用这些关联预测基于过去观察和预测错误的未来值ARIMA术语定义使用
1) 静止性:时间序列分析中最重要的概念之一是静态性静止性发生时时间变换不改变数据分布形状相形之下非静止数据点有方法、差异和共变随时间变化。这意味着数据有趋势、循环、随机行走或三大组合预测学通则非静止数据不可预测,无法建模
运行ARIMA数据需要静止时间序列稳定化 时间变换不改变分布形状基本属性分布如平均值、差异和共差随时间变化不变外行语中,你需要通过删除系统化组件导出数据静态性,使数据随机显示表示你必须变换非静止数据集使用ARIMA有两种不同的静态违反,理解他们时,理解定点性.有2种技术导出静态性, 幸运的是ARIMA使用差分方法诱导静态性, 即ARIMA方程本身有两种不同的测试叫作ADF系统并KPSS测试检查数据是否静止运行测试后,通过适当转换数据诱导静态,直至静止
2) 异变:数据变换需要减点t时间t相异取法表示减时t值t下图应用判别顺序一令令数据静止所有这些都可以在多编码库和包中实现
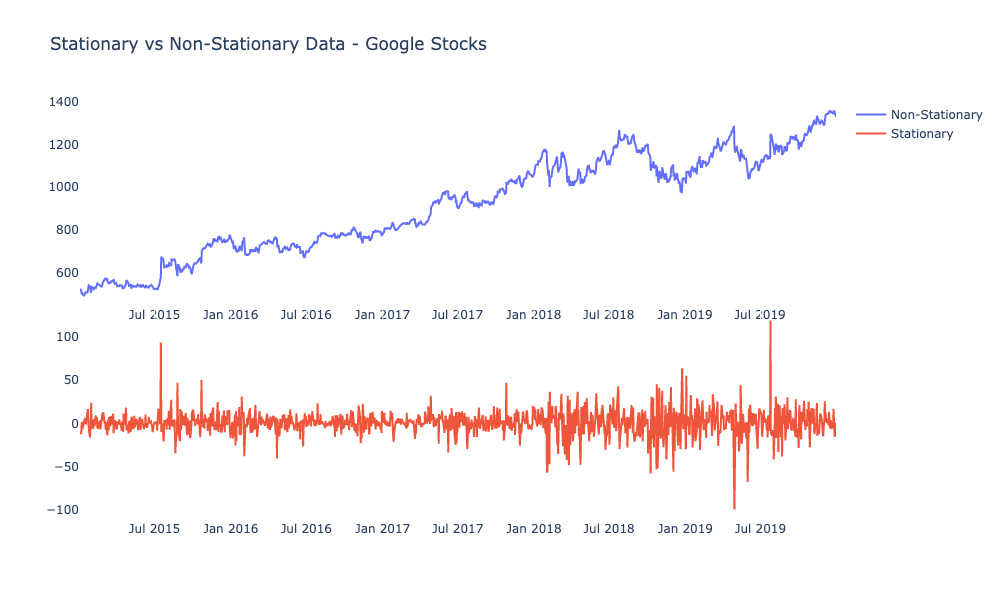
3) 自动回归拉格:这些是静止时间序列历史观察
ARIMA自动回归部分与数据历史方面相关联自回归延时前一数据点自动回归延时指前两个数据点等这是ARIMA关键分量,此分量将显示前数据点中有多少值,您想在编译下一个预测数据点时加以考虑。确定模型内自回归延时数的实用技巧是自相关局部自相关图
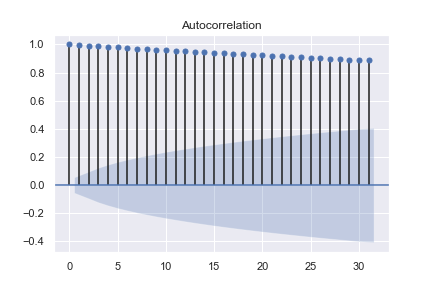
举个例子,请见下方自相关图和局部自相关图第二点后下降表示ARIMA模型使用2自回归延时
4) 运动平均拉与历史预测错误窗口相关
移动平均延时指窗口大小,您培训模型时用它计算预测错误移动平均延迟表示前两个数据点的平均误差帮助纠正数据点预测移动平均延时数说明窗口大小窗口大小会增加数据点误差数,供下次预测使用重覆,确定与自相关和局部自相关方块使用多延时有效深入分析自回归拉动平均拉动理解时差.
5)拉格顺序说明多少段回程延时顺序一表示前一观察是预测方程的一部分
八.剖析ARIMA和泛方程
现在你们知道通用定义和术语,我将讨论这些定义如何连接ARIMA方程本身下图泛称ARIMA模型,并用术语校准模型每种参数都改变模型计算法
以下是ARIMA总参数
ARIMA(p,d,q)~自反综合移动平均值(AR,I,MA)
P-顺序自回归式时差(AR部件)
D-顺序歧义(整合部分,I)
q-serve移动平均时差(ma部分)
下方为ARIMA通用公式显示参数使用方式分解每一参数和这些参数与方程的相容性

1)-自回归延时排序
等p=2和所有东西0-ARIMA20/0使用前2个数据点帮助最终预测下方程中可以注意到这一点,并分解出整个ARIMA方程
![]()
方程提供预测 特定时间,如果你使用p顺序2自回归延时使用前2个数据点和时段水平预测举例说,下红色值用于预测下一点,这将是绿线上的第一个数据点

2-分判顺序(归并部分,I)
ARIMA中下一个参数为d参数,该参数还分判部分或集成部分前面提到过,你需要差分数据固定化拥有非静止数据时,ARIMA可帮助应用辨别法直到数据静止ARIMA模型中的d术语为您使用此判别法应用d=1时按顺序对数表示你曾经有分歧应用d=2时差二倍只求差到数据最终静态如前所述,你可以检查数据是否静止使用ADF系统并KPSS测试下方方程对齐通知三四可应用

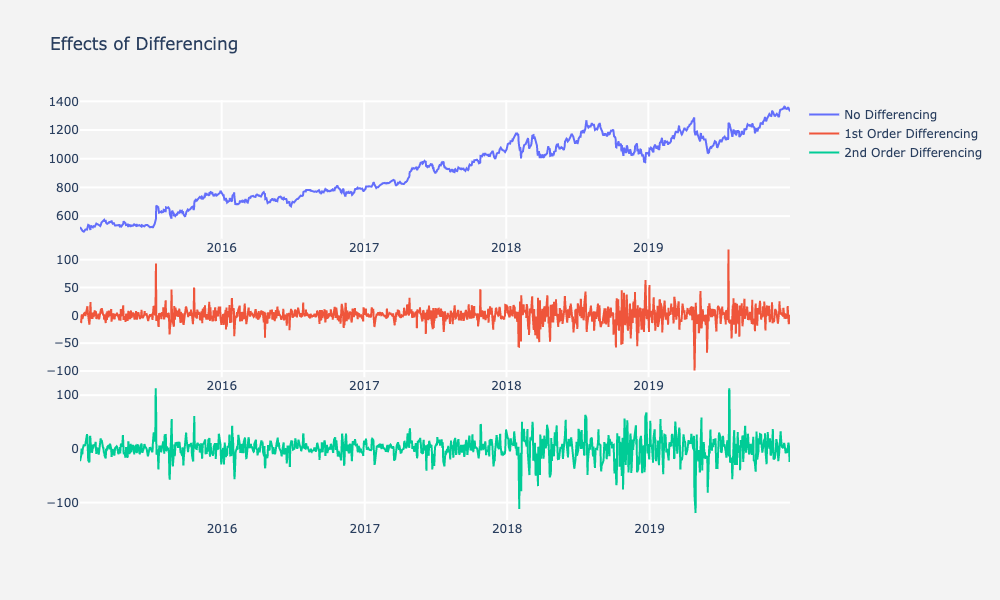
应用第一阶分时不修改自回归延时或移动平均数时,ARIMA(01.00)也称a随机步行.表示模型生成预测时不计前几个数据点预测随机生成

3q-移动平均时差排序
最后,我们将讨论q术语q术语为移动平均部分,并应用到想查看预测错误时错误输入时间t数据训练时此点相关可使用此参数校正前次预测中的错误,用于新预测下方程错误术语使用
![]()
下图显示ARIMA(0,0,3)三个红色数据点表示窗口大小帮助预测下一点下从三大红点预测点将是绿线上的第一个数据点

九.测量预测值是否正确
一号火车测试拆分
现在你知道ARIMA所有组件后,我将讨论如何确保您的预测良好。训练模型时,需要将数据划分为火车测试集这样你就可以评价测试集, 因为这组值没有在模型适配期间训练相对于其他经典机学习技术,即随机分割数据,时间序列必须是顺序火车测试拆分下图典型火车测试拆分
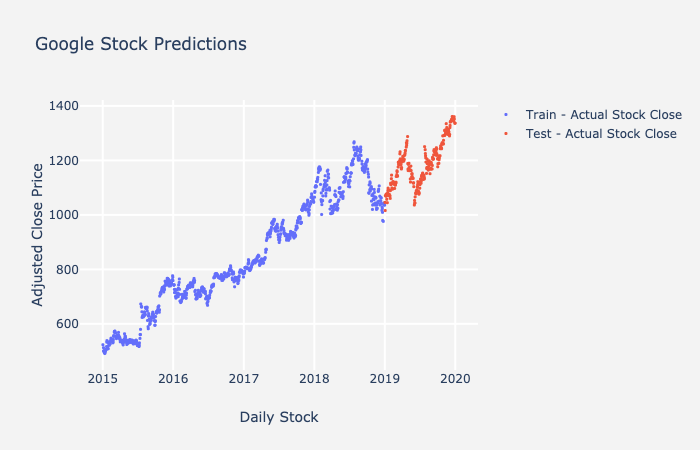
2模型预测错误
完成训练模型后,你需要知道预测距离实际值多远出错度量测试集预测使用各种误差度量计算离实际值有多远目标预测尽可能减少误差这一点很重要 因为它能说明预测有多好了解预测错误也有助于调整ARIMA模型参数
平均绝对误差和绝对百分数误差平均绝对误差单数表示平均预测距离实际值平均百分数误差(MAPE)是我们使用的另一个尺度,平均平均误差表示百分比说明模型的精确性MAE和MAPE方程下方和Google数预测图列火车测试拆分可使用下文方程计算预测错误通知使用紫线预测值和红色数据点帮助计算测试集MAE和MAPE
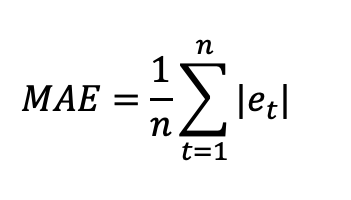


上方示例图中,线表示模型适配预测值,点表示实数据值获取时点平均绝对误差时,从预测中减去实际数据(图中点表示线)获取误差归并除以总点数测试集预测平均绝对误差72.35, 平均表示每次误差约72.35平均绝对百分数误差5.89%,这说明模型总体精确度约94.11%
ARIMA调优步骤概述
深入了解所有步骤后,我将概述你想如何思考每一个参数和步骤来训练ARIMA模型
1)表示变法顺序d使用静态测试
2)自回归术语排序,p使用ACF图象卢布斯
3)识别移动平均值q使用ACF图象卢布斯
4) 优化模型以尽量减少测试数据误差使用平均值绝对误差并平均值绝对百分比误差完成火车测试后拆分
X.多变预测:简单归纳
现在你知道调优ARIMA基础教程后,我想再提一个有趣的题目上面详细描述的一切都与预测一个变量有关univariate时间序列另一种重要概念产生时,想预测多变量即多变量预测将是一个重要概念, 我在博客系列第3部分讲时间序列, 介绍Cisco使用案例
为什么要将更多变量引入时序数据集中的其他变量有可能帮助解释或帮助预测目标变量未来值我们称这些引导指示器.引导指示器在趋势启动后发信号并命令你注意
举个例子 假设你开冰淇淋店 夏令营PG&E切断电源估计未来冰淇淋销售会下降无电存储冰淇淋开关电源 将是一个大例子 领先指标可使用此指标补充预测未来销售量
多变量ARIMAX和向量自回归下一篇文章将简单谈ARIMAX

时间序列博客第二部分详解ARIMA及其组件内第三部分Cisco使用案例 预测Cisco设备内存分配
ARIMA经验如何最喜欢用什么方式实现通知我评论

连接CISCO